Ecuaciones de segundo grado
En general, las ecuaciones de segundo grado son aquellas donde la x aparece elevada a 2 en alguno de sus términos.
Pueden ser ecuaciones de segundo grado completas o incompletas, en función de si tienen todos su términos o no. Aquí me voy a centrar en explicarte las ecuaciones de segundo grado completas.
Qué son las ecuaciones de segundo grado completas.
Las ecuaciones de segundo grado completas o ecuaciones cuadráticas son las que se representan de la siguiente forma:
Donde a, b y c son las constantes de la ecuación:
- a es el número que va siempre delante de x al cuadrado.
- b es el número que va siempre delante de la x.
- c es el número.
Es decir, las ecuaciones de segundo grado completas son las que tienen término con x elevada a 2, término con x elevada a 1 (o simplemente la x). Si faltara alguno de estos términos, estaríamos hablando de ecuaciones de segundo grado incompletas, que se resuelven con otro procedimiento distinto.
En la primera lección del curso de ecuaciones de segundo grado, comento más detalladamente cómo reconocer una ecuación de segundo grado
Al ser ecuaciones de segundo grado, tienen 2 soluciones. Recuerda que el grado de una ecuación es igual al número de soluciones.
Cómo resolver ecuaciones de segundo grado completas.
En este vídeo tienes ejercicios resueltos paso a paso sobre ecuaciones de segundo grado completas:
Y a partir de aquí te lo explico todo más despacio:
Identificación de constantes en la ecuación de segundo grado.
El primer paso para resolver ecuaciones de segundo grado completas es identificar las constantes correctamente. Como hemos dicho antes, las constantes son los números que van delante de x al cuadrado, x y el término que no lleva x.
Vamos a verlo en un ejemplo:
En este caso, delante de x al cuadrado, no hay nada, por tanto a = 1.
Delante de x hay un 5, por lo que b=5.
Y el término que no lleva x es un 4, por lo que c=4.
Recuerda que cuando no hay nada delante de las incógnitas, es porque están multiplicadas por 1, o en otras palabras, equivale a que haya un 1 delante. En el curso de cómo resolver ecuaciones de segundo grado, se explica paso a paso cómo hacerlo para que no te equivoques.
Ahora, si nos damos cuenta, la ecuación es ligeramente diferente, pero que es causa de muchos errores si no estamos atentos. Veamos por qué:
En la forma general no hay ningún signo menos:
Por tanto, debemos de transformar nuestra ecuación para que esté de la misma forma que la forma general de las ecuaciones de segundo grado completas:
Ahora ya la tenemos de la misma forma, donde no aparece ningún signo menos y entonces a, b y c se obtiene igual que en el primer caso:
Cuando tengamos más práctica, identificaremos las constantes directamente, sin necesidad de transformar nuestra ecuación, pero para empezar es una muy buena forma de evitar errores.
Fórmula general de ecuaciones de segundo grado completas.
Una vez identificadas las constantes, para resolver las ecuaciones de segundo grado completas hay que aplicar la siguiente fórmula:
Vamos a ver como se utiliza, resolviendo los ejemplos anteriores:
Tenemos la primera ecuación de segundo grado, en la que hemos identificado las constantes:
Ahora, tenemos que sustituir el valor de cada constate en la fórmula general:
Y ahora operamos, dentro de la raíz, teniendo en cuenta la jerarquía de operaciones:
Llegados a este punto, tenemos que resolver por un lado el signo + y por el otro el signo – :
Luego las dos soluciones sería -1 y -4. Si tuviéramos el caso de que las fracciones no fueran exactas, habría que simplificarlas.
Mucho cuidado con los signos – de las constantes. En el curso de cómo resolver ecuaciones de segundo grado, explico más detalladamente cómo resolver paso a paso cuando se nos presenta este caso. Es una de las causas de que no llegar al resultado correcto.
Existen casos particulares donde el resultado de la raíz es negativo, o que sus soluciones no son exactas o bien el resultado de la raíz no es exacto.
Solución de ecuaciones de segundo grado
Ecuaciones de segundo grado con soluciones en forma de raíz
Las soluciones de una ecuación de segundo grado no tienen por qué ser dos números enteros distintos. En algunos casos, pueden tener una solución doble o tener dos soluciones complejas.
Muchas veces cuando las soluciones no son enteras, empiezas a dudar si tu solución es correcta o no.
Y ahora, vamos a ver cómo pueden ser las soluciones de una ecuación de segundo grado.
Nos encontramos con este caso cuando la raíz no tiene una solución entera. Como norma general, se dejará en forma de raíz para no tener que operar con decimales, aunque si estamos resolviendo un problema y se necesita el resultado exacto, no tendremos más remedio que resolver la raíz cuadrada con la calculadora
Por ejemplo, tenemos la siguiente ecuación de segundo grado:
![]()
El primer paso es resolver la ecuación de segundo grado mediante la fórmula general:
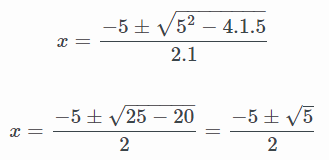
Llegados a este punto, vemos que la raíz de 5 no tiene solución exacta. Por tanto, matemáticamente, se deja en forma de raíz:
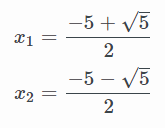
No es obligatorio dejarlo en forma de raíz, pero es más cómodo dejarlo así, para no tener que arrastrar decimales. El resultado podría darse con decimales y estaría igual de correcto. Ocurre lo mismo que con las fracciones, que cuando un resultado no da exacto, se deja en forma de fracción.
Ecuaciones de segundo grado con solución doble
Cuando estamos resolviendo una ecuación de segundo grado y el resultado de la raíz o el discriminante es 0, se dice que tenemos una solución doble, ya que vamos a tener la misma solución repetida 2 veces. Veamos cómo actuar en este caso:
![]()
Como a priori no sabemos cómo van a ser las soluciones, resolvemos la ecuación como cualquier otra: 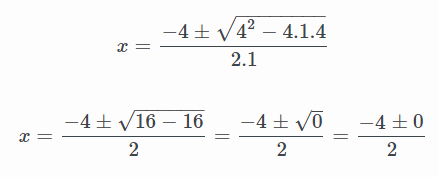 Al llegar a esta parte de la resolución, vemos el resultado de la raíz es 0.
Al llegar a esta parte de la resolución, vemos el resultado de la raíz es 0.
Un grave error es dejar solamente 1 solución. Esto nunca lo hagáis porque estaréis suspensos directamente. Lo que se hace en estos casos es trabajar con el 0:
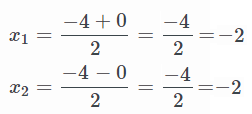
Se resuelve siguiendo el procedimiento habitual, aunque parezca obvio sumar y restar 0, pero es una buena forma de llegar a las 2 soluciones.
Otra forma de indicar las soluciones es desarrollar la fórmula general hasta el final, llegar a una solución pero indicar con letra de que se trata de una solución doble.

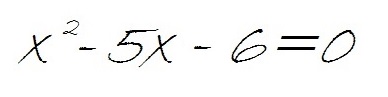

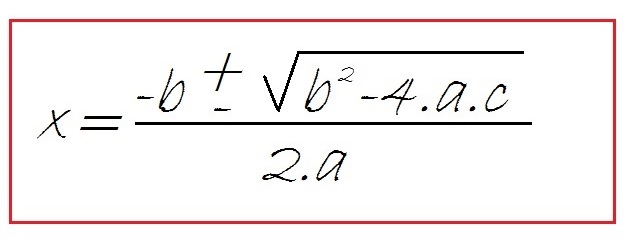

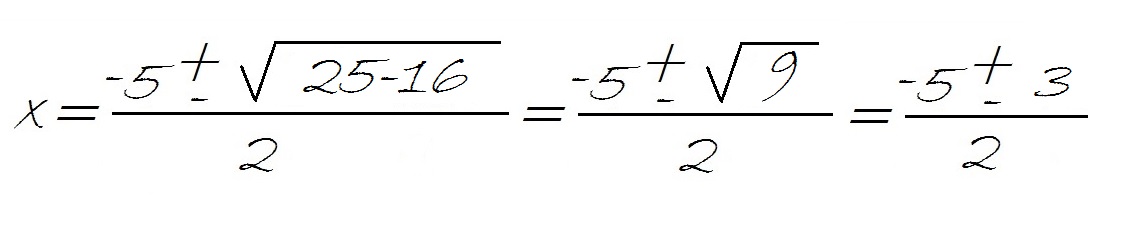

Comentarios
Publicar un comentario