Sistema de Ecuaciones

Empecemos directamente definiendo que un sistema de ecuaciones es un conjunto de dos o más ecuaciones que contiene a dos o más incógnitas, dichas ecuaciones tienen relación entre sí ya que el valor de las incógnitas satisfacen todas las ecuaciones al mismo tiempo.

Para esta ocasión estudiaremos los sistemas de ecuaciones 2x2 (2 ecuaciones y 2 incógnitas). Este tipo de sistemas es muy frecuente en tareas de la escuela, en exámenes de admisión y son tan versátiles que pueden ser usadas sin ningún problema para representar casos reales. Existe muchas maneras de resolver un problema de este tipo, algunas un poco más difíciles y complicadas que otras, pero en esta página nos centraremos en dos maneras distintas que se ven durante toda la secundaria, es decir: la forma algebraica y la forma gráfica.

La primera se desglosa en varios procedimientos algebraicos distintos: El método de reducción (también conocido como de suma y resta), el método de sustitución y el método de igualación; y por otra parte el método gráfico consiste en interpretar y analizar de forma gráfica el comportamiento de ambas ecuaciones en un mismo plano cartesiano.

Empecemos analizando los método algebraicos y como usarlos:

Método de suma y resta

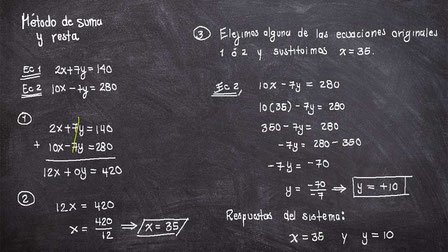
El método se suma y resta, también conocido como de reducción, es un método donde lo que se busca es eliminar una de las dos incógnitas mediante el uso de una suma algebraica. Esta eliminación puede darse de dos manera:

 

1.- La manera directa es cuando nos damos cuenta que en ambas ecuaciones del sistema, la misma incógnita tiene el mismo coeficiente solo que con signo contrario, como se puede observar en la imagen (da click para ver la imagen a pantalla completa). Si se diera este caso el primer paso es colocar ambas ecuaciones una encima de la otra de manera que cada tipo de incógnita forme una columna al igual que la parte sin incógnita (que debe estar siempre a la derecha del igual).

 

Posteriormente sumamos como aprendimos en secciones anteriores y nos damos cuenta que una incógnita se elimina pues su coeficiente se vuelve cero como en el ejemplo. A continuación resolvemos la ecuación de primer grado que hemos creado para obtener el valor de la primera literal.

Como paso final sustituimos dicho valor en una de las ecuaciones originales, para ello donde se encuentre dicha letra usamos paréntesis y colocamos su valor dentro de estos, realizamos las operaciones correspondientes para resolver esta segunda ecuación de primer grado y de esta manera obtendremos la segunda literal.

 

Con esto quedaría resuelto nuestro sistema de ecuaciones en donde la respuesta sería el valor de ambas literales al mismo tiempo.

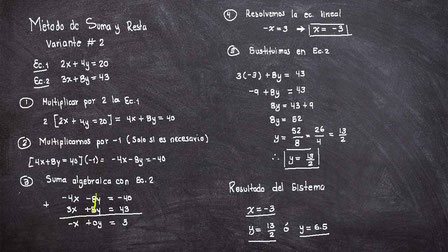
2.- Detectando múltiplo: Esta forma procede cuando hay una relación entre alguna de las dos letras en ambas ecuaciones en cuanto si a múltiplos de sus coeficientes estamos hablando. Un ejemplo sería que una ecuación fuera 2x+4y=20 y que la otra fuera 3x+8y=43 en donde la incógnita y en ambos casos tiene coeficientes múltiplos de 4.

En este método no importa si los coeficientes sean de signos contrarios, únicamente nos importan que sean múltiplos.

El procedimiento comienza de la siguiente manera (puedes verlo con números en la imagen de la izquierda).

 

Algo muy importante de este método es que su propósito es lograr eliminar una de las incógnitas de ambas ecuaciones para encontrar la que no se ha eliminado. De esta manera y al obtener la segunda incógnita podemos usar ese resultado para encontrar la primera que hemos eliminado. Por ello en este método se suma algebraícamente para lograr dicho propósito.

Método de Sustitución

Al igual que con la comida podemos elegir la bebido con que acompañarla, los sistemas de ecuaciones tienen distintas maneras o métodos de ser resueltos y esta en ti elegir el que te parezca más sencillo, con el que sientas más confianza, etc. y no tendrás ningún problema en absoluto ya que las respuestas siempre serán las mismas.

Un ejemplo de ello es resolver el primer sistema de ecuaciones de arriba usando el método de sustitución, como se puede apreciar en la imagen de la izquierda.

El método de sustitución consiste en el procedimiento de despeje de una variable (letra) de una de las 2 ecuaciones y sustituir el resultado en la segunda ecuación (la que no elegimos primero), de esta manera los pasos a seguir (que puedes ver con detalle en la imagen) serían los siguiente:

 

1.- Despejar una incógnita en solo una de las ecuaciones (elige la que sea mas sencilla de despejar).

2.- Hecho el despeje procedemos abrir paréntesis en la segunda ecuación en los lugares donde se encuentre la letra que despejamos en el punto 1.

3.- Dentro de los paréntesis, colocamos el resultado del despeje del punto 1.

4.- Resolvemos la ecuación de primer grado que se ha creado para obtener el valor de la segunda incógnita.

5.- Con el valor del paso 4 regresamos a donde teníamos el despeje en el punto 2 y colocamos dicho valor (paso 4) para encontrar la primera ecuación.

6.- Comprobamos sustituyendo los valores al mismo tiempo en alguna de las ecuaciones originales.

 

Como puedes observar en la imagen, el resultado del sistema de ecuaciones es y=10 y x=35, que es exactamente el mismo resultado que el método de suma y resta, con lo que se comprueba que no importa que método elijas siempre llegarás al mismo resultado. Esta característica te puede ayudar a averiguar si realizaste mal un cálculo en algún otro método ya que debería darte el mismo resultado.

Por último, demostremos este mismo punto mediante el siguiente método de solución...

Método de igualación

Este método suele ser sencillo para aquellos que el despeje se les facilita. 

El método recibe el nombre del hecho que, para resolver el sistema de ecuaciones debemos despejar la misma letra en ambas ecuaciones, esto con el motivo de igualar la parte de la derecha de la igualdad y resolver una ecuación de primer grado con la misma incógnita en ambos lados.

En la imagen de la izquierda podemos observar el mismo sistema de ecuaciones que se resolvió anteriormente, la diferencia con el método de sustitución anterior es que aquí se despeja la X para ambas ecuaciones, de esta manera se igualan las partes derechas de los despejes para finalmente encontrar el valor de la y.

Encontrando el valor de y podemos sustituirlo en cualquiera de los 2 despejes de x para encontrar el valor de esta misma letra, para este caso (como en los anteriores) el resultado es y=10 y x=35.

Aprendamos con la práctica

A continuación te presento un quiz en el que podrás poner a prueba los conocimiento adquiridos en este tema.